
(png)
(png)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.tri as mtri
# u, v are parameterisation variables
u = (np.linspace(0, 2.0 * np.pi, endpoint=True, num=50) * np.ones((10, 1))).flatten()
v = np.repeat(np.linspace(-0.5, 0.5, endpoint=True, num=10), repeats=50).flatten()
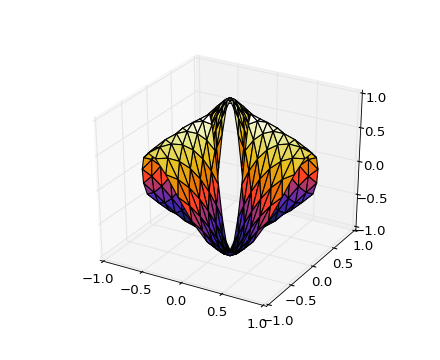
# This is the Mobius mapping, taking a u, v pair and returning an x, y, z
# triple
x = (1 + 0.5 * v * np.cos(u / 2.0)) * np.cos(u)
y = (1 + 0.5 * v * np.cos(u / 2.0)) * np.sin(u)
z = 0.5 * v * np.sin(u / 2.0)
# Triangulate parameter space to determine the triangles
tri = mtri.Triangulation(u, v)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
# The triangles in parameter space determine which x, y, z points are
# connected by an edge
ax.plot_trisurf(x, y, z, triangles=tri.triangles, cmap=plt.cm.Spectral)
ax.set_zlim(-1, 1)
# First create the x and y coordinates of the points.
n_angles = 36
n_radii = 8
min_radius = 0.25
radii = np.linspace(min_radius, 0.95, n_radii)
angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False)
angles = np.repeat(angles[...,np.newaxis], n_radii, axis=1)
angles[:,1::2] += np.pi/n_angles
x = (radii*np.cos(angles)).flatten()
y = (radii*np.sin(angles)).flatten()
z = (np.cos(radii)*np.cos(angles*3.0)).flatten()
# Create the Triangulation; no triangles so Delaunay triangulation created.
triang = mtri.Triangulation(x, y)
# Mask off unwanted triangles.
xmid = x[triang.triangles].mean(axis=1)
ymid = y[triang.triangles].mean(axis=1)
mask = np.where(xmid*xmid + ymid*ymid < min_radius*min_radius, 1, 0)
triang.set_mask(mask)
# tripcolor plot.
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.plot_trisurf(triang, z, cmap=plt.cm.CMRmap)
plt.show()
Keywords: python, matplotlib, pylab, example, codex (see Search examples)